Lab 5: Marked point patterns
This session covers modelling of marked point patterns using marked point processes. The lecturer’s R script is available here (right click and save).
library(spatstat)
Exercise 1
The dataset spruces contains the Norwegian Spruces dataset giving the locations of trees and their diameters at breast height.
-
Read the help file for the data;
-
access the dataset and plot it;
plot(spruces)
-
re-plot the data so that the tree diameters are displayed at a physical scale that is 10 times the physical scale of the location coordinates.
plot(spruces, markscale = 10)
-
use
Smooth(notice the upper case S) to compute and plot a pixel image of the local average tree diameter;plot(Smooth(spruces, sigma = 8))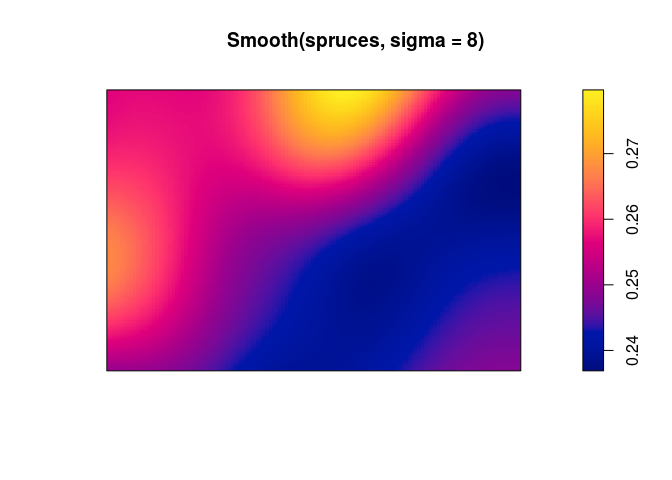
-
trees are normally classified as ‘adult’ when their diameter exceeds 30 centimetres. Use the
cutcommand to classify each tree as adult or juvenile, and produce a multitype point pattern in which the trees are marked as adult or juvenile. Plot this pattern, and plot the adults and juveniles separately.cutspruces <- cut(spruces, breaks = c(0,0.3,0.4), labels = c("juvenile", "adult")) plot(cutspruces, main = "")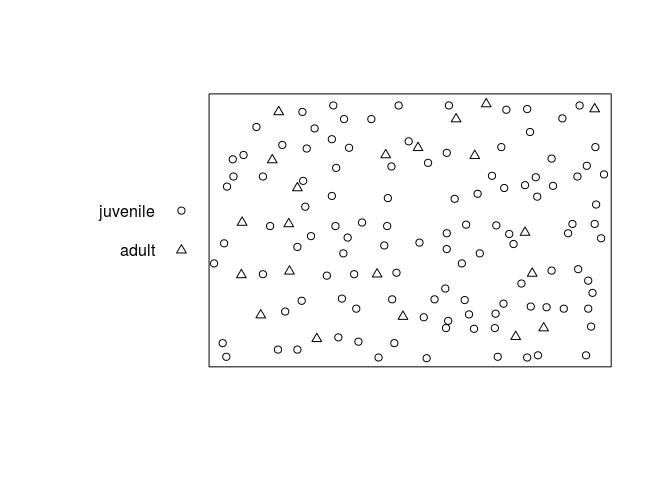
plot(split(cutspruces), main = "")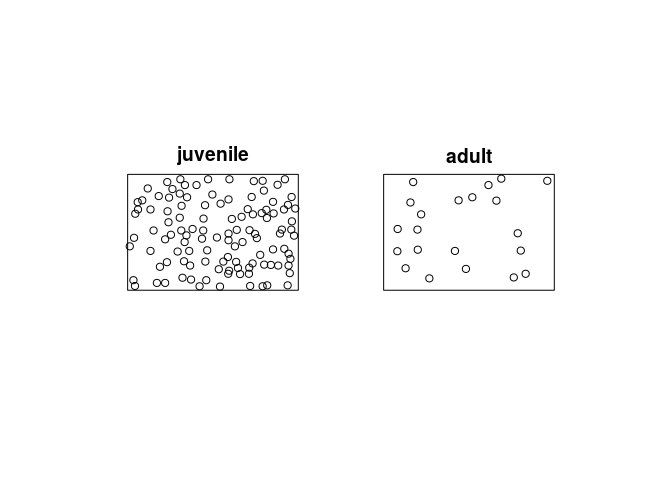
Exercise 2
The file anthills.txt is available in the Data directory on github and downloadable by this direct link (right click and save).
It records the locations of anthills recorded in a 1200x1500 metre study region in northern Australia. Coordinates are given in metres, along with a letter code recording the ecological ‘status’ of each anthill.
-
read the data into
Ras a data frame, using theRfunctionread.table. (Since the input file has a header line, you will need to use the argumentheader=TRUEwhen you callread.table.)dat <- read.table(file = "../Data/anthills.txt", header = TRUE) -
check the data for any peculiarities.
-
create a point pattern
hillscontaining these data. Ensure that the marks are a factor, and that the unit of length is given its correct name.hills <- with(dat, ppp(x, y, xrange = c(0, 1200), yrange = c(0, 1500), marks = status, units=c("metre", "metres"))) -
plot the data.
plot(hills, main = "")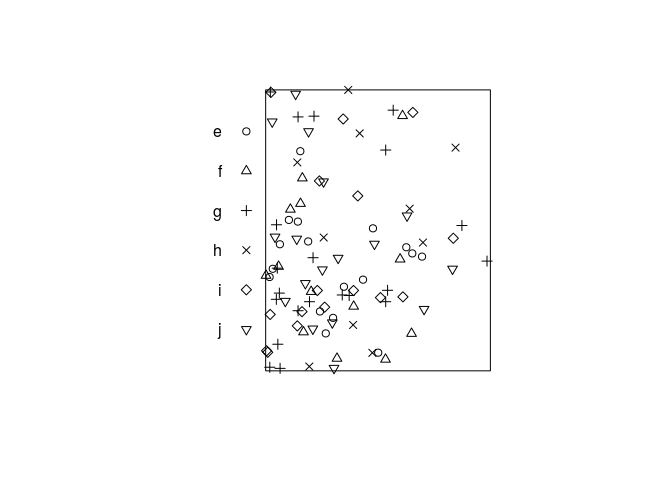
Exercise 3
The dataset hamster is a multitype pattern representing the locations of cells of two types, dividing and pyknotic.
-
plot the data;
plot(hamster)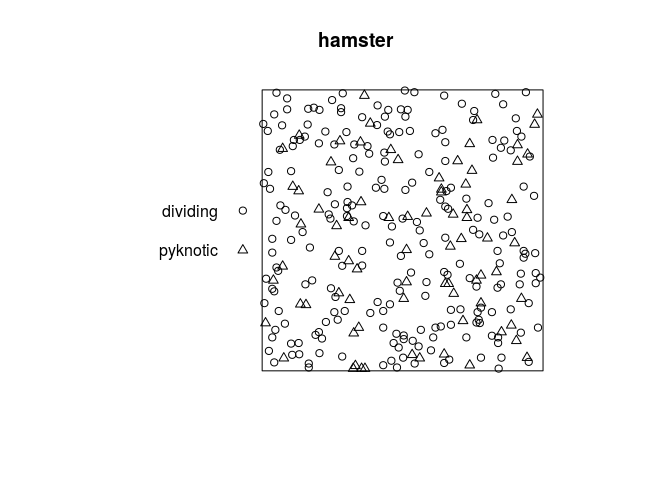
-
plot the patterns of pyknotic and dividing cells separately;
plot(split(hamster), main = "")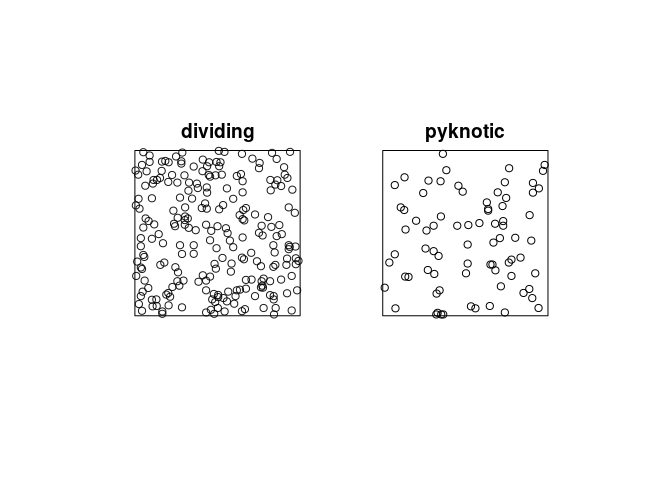
-
plot kernel estimates of the intensity functions of pyknotic and dividing cells separately;
plot(density(split(hamster)), main = "")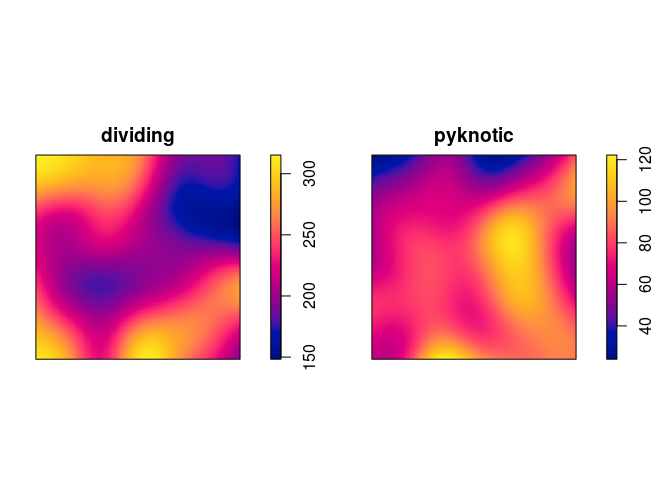
-
use
relriskto perform cross-validated bandwidth selection and computation of the relative intensity of pyknotic cells.plot(relrisk(hamster, hmax = 1, relative = TRUE, control = "dividing"))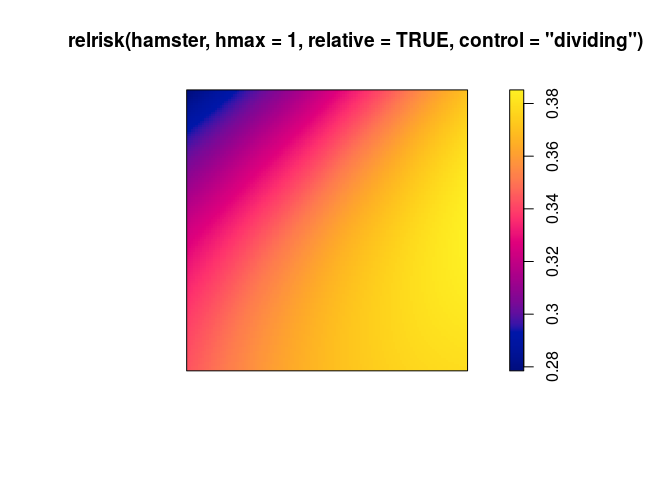
Exercise 4
The command rmpoispp generates simulated realisations of a multitype Poisson process. The first argument lambda specifies the intensity function λ(x, y, m) which gives the intensity of points at location (x,y). It may be given in several forms.
-
If
lambdais a single number, it specifies the intensity of points of each type. Try computing, inspecting and plotting the result ofrmpoispp(21, win=square(1), types=c("yes", "no"))What is the expected total number of points generated by this command?
X <- rmpoispp(21, win=square(1), types=c("yes", "no")) summary(X)## Marked planar point pattern: 45 points ## Average intensity 45 points per square unit ## ## Coordinates are given to 8 decimal places ## ## Multitype: ## frequency proportion intensity ## yes 22 0.4888889 22 ## no 23 0.5111111 23 ## ## Window: rectangle = [0, 1] x [0, 1] units ## Window area = 1 square unitplot(X, main = "")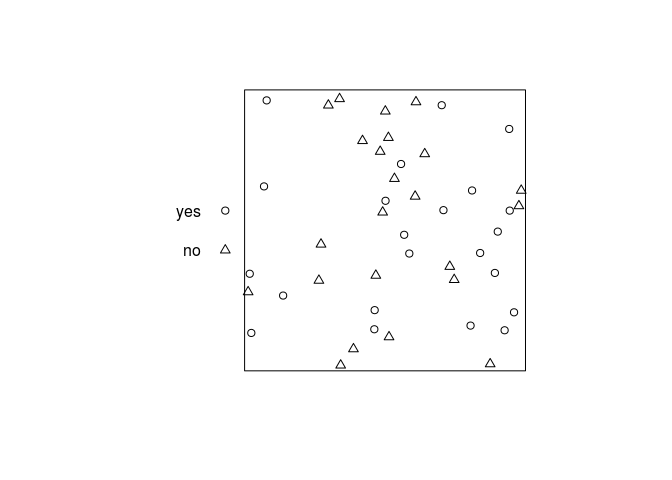
We expect 2 × 21 = 42 points on average.
-
If
lambdais a vector of numbers, the vector entries specify the intensities for each type of point. Tryrmpoispp(c(20,40,20), types=letters[1:3])What is the expected total number of points generated by this command?
rmpoispp(c(20,40,20), types=letters[1:3])We expect 20 + 40 + 20 = 80 points on average in this case.
-
If
lambdais a function with argumentsx,y,mthen this is interpreted as the intensity function λ(x, y, m). Tryfun <- function(x,y,m) { 40 * (x+y) } X <- rmpoispp(fun, types=letters[24:26]) fun2 <- function(x,y,m) { ifelse(m == "yes", 100 * x, 50 * (1-x)) } X2 <- rmpoispp(fun2, types=c("yes", "no"))What is the expected total number of points in
X?We expect 3 ⋅ ∫[0, 1]∫[0, 1]40(x + y)dxdy = 120 points on average in this case.
Exercise 5
Take the Harkness-Isham ants’ nests data ants
-
use
summaryto estimate the average intensities of the points of each type.summary(ants)## Marked planar point pattern: 97 points ## Average intensity 0.0002261486 points per square unit (one unit = 0.5 ## feet) ## ## Coordinates are integers ## i.e. rounded to the nearest unit (one unit = 0.5 feet) ## ## Multitype: ## frequency proportion intensity ## Cataglyphis 29 0.2989691 6.761144e-05 ## Messor 68 0.7010309 1.585372e-04 ## ## Window: polygonal boundary ## single connected closed polygon with 11 vertices ## enclosing rectangle: [-25, 803] x [-49, 717] units ## Window area = 428922 square units ## Unit of length: 0.5 feet ## Fraction of frame area: 0.676lam <- intensity(ants) -
Generate and plot a realisation of a marked Poisson process in the same window as the data, with the same possible types of points, with uniform intensities for each type, given by the intensities estimated from the data.
rmpoispp(lam, win = Window(ants), types = names(lam))## Marked planar point pattern: 69 points ## Multitype, with levels = Cataglyphis, Messor ## window: polygonal boundary ## enclosing rectangle: [-25, 803] x [-49, 717] units (one unit = 0.5 feet)Or the even shorter
rmpoispp(lam, win = Window(ants))## Marked planar point pattern: 98 points ## Multitype, with levels = Cataglyphis, Messor ## window: polygonal boundary ## enclosing rectangle: [-25, 803] x [-49, 717] units (one unit = 0.5 feet) -
Repeat the simulation several times. Do the simulations look like the data?
Make 11 simulations:
simants <- rmpoispp(lam, win = Window(ants), types = names(lam), nsim = 11)Add original data as list item number 12:
simants[[12]] <- antsPlot them all:
plot(simants, legend = FALSE, main = "")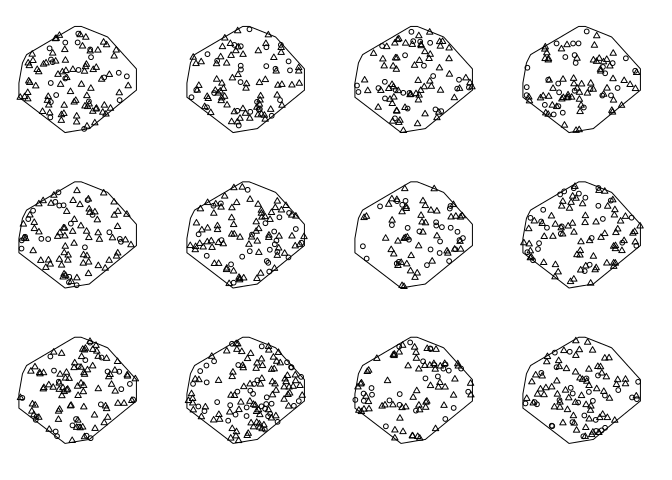
Exercise 6
Here we will fit multitype Poisson point process models to the Harkness-Isham ants’ nests data ants.
-
Fit the model
ppm(ants ~ marks)and interpret the result. Compare the result withsummary(ants)and explain the similarities.fit1 <- ppm(ants ~ marks)This is a Poisson model with a separate constant intensity for each mark. The fitted intensities are:
exp(coef(fit1)[1])## (Intercept) ## 6.762949e-05exp(coef(fit1)[1] + coef(fit1)[2])## (Intercept) ## 0.0001585795This agrees perfectly with the output of
summary(ants):summary(ants)## Marked planar point pattern: 97 points ## Average intensity 0.0002261486 points per square unit (one unit = 0.5 ## feet) ## ## Coordinates are integers ## i.e. rounded to the nearest unit (one unit = 0.5 feet) ## ## Multitype: ## frequency proportion intensity ## Cataglyphis 29 0.2989691 6.761144e-05 ## Messor 68 0.7010309 1.585372e-04 ## ## Window: polygonal boundary ## single connected closed polygon with 11 vertices ## enclosing rectangle: [-25, 803] x [-49, 717] units ## Window area = 428922 square units ## Unit of length: 0.5 feet ## Fraction of frame area: 0.676 -
Fit the model
ppm(ants ~ marks + x)and write down an expression for the fitted intensity function.fit2 <- ppm(ants ~ marks + x) (co <- coef(fit2))## (Intercept) marksMessor x ## -9.5243832518 0.8522118655 -0.0002041438Intensity for the reference type (Cataglyphis):
λ((x, y)) = exp(−9.5243833 + −2.0414381 × 10−4 ⋅ x)
Intensity for the other type (Messor):
λ((x, y)) = exp(−9.5243833 + 0.8522119 + −2.0414381 × 10−4 ⋅ x)
-
Fit the model
ppm(ants ~ marks * x)and write down an expression for the fitted intensity function.fit3 <- ppm(ants ~ marks * x) (co <- coef(fit3))## (Intercept) marksMessor x marksMessor:x ## -9.605698e+00 9.676854e-01 1.107981e-05 -3.071343e-04Intensity for the reference type (Cataglyphis):
λ((x, y)) = exp(−9.605698 + 1.1079805 × 10−5 ⋅ x)
Intensity for the other type (Messor):
λ((x, y)) = exp(−9.605698 + 0.9676854 + (1.1079805 × 10−5 + 0.9676854)⋅x)
-
Compute the fitted intensities of the three models fitted above using
predictand plot the results.pred <- c(predict(fit1), predict(fit2), predict(fit3)) plot(as.solist(pred), ncols = 2, main = "")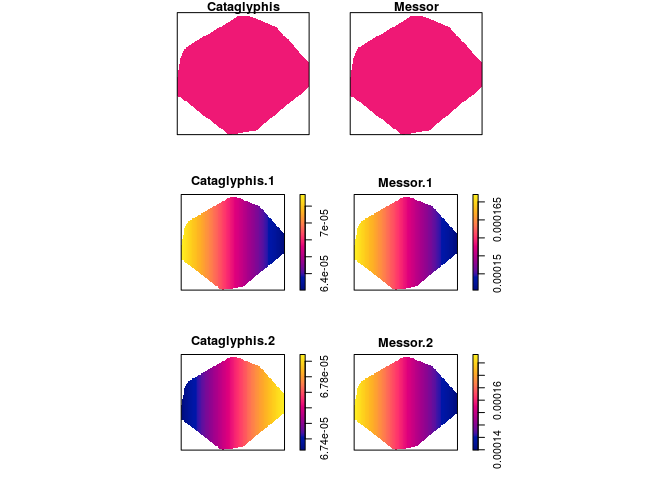
-
Explain the difference between the models fitted by
ppm(ants ~ marks + x)andppm(ants ~ marks * x).For the additive model the effect of the
xcoordinate is the same for both types of ants, while the effect ofxdiffers in the multiplicative model.
Exercise 7
The study region for the ants’ nests data ants is divided into areas of ‘scrub’ and ‘field’. We want to fit a Poisson model with different intensities in the field and scrub areas.
The coordinates of two points on the boundary line between field and scrub are given in ants.extra$fieldscrub. First construct a function that determines which side of the line we are on:
fs <- function(x,y) {
ends <- ants.extra$fieldscrub
angle <- atan(diff(ends$y)/diff(ends$x))
normal <- angle + pi/2
project <- (x - ends$x[1]) * cos(normal) + (y - ends$y[1]) * sin(normal)
factor(ifelse(project > 0, "scrub", "field"))
}
Now fit the models:
ppm(ants ~ marks + side, data = list(side=fs))
ppm(ants ~ marks * side, data = list(side=fs))
and interpret the results.
fit1 <- ppm(ants ~ marks + side, data = list(side=fs))
fit2 <- ppm(ants ~ marks * side, data = list(side=fs))
In the first model the fitted intensity is lower in the scrub than in the field (but this effect is not significant).
In the second model the fitted intensity of Cataglyphis is lower in the scrub than the intensity of Cataglyphis in the field, where as it is the other way around for Messor. When we allow for the different effect between ant types the scrub/field covariate is significant.