Melb2018

Lab 10: Gibbs processes

This session is concerned with Gibbs models for point patterns with interpoint interaction. The lecturer’s R script is available here (right click and save).

library(spatstat)

## Loading required package: spatstat.data

## Loading required package: methods

## Loading required package: nlme

## Loading required package: rpart

## 
## spatstat 1.56-1.007       (nickname: 'Damn You Autocorrect') 
## For an introduction to spatstat, type 'beginner'

Exercise 1

In this question we fit a Strauss point process model to the swedishpines data.

We need a guess at the interaction distance (R). Compute and plot the (L)-function of the dataset and choose the value (r) which maximises the discrepancy (\lvert L(r)-r \rvert).

We plot the above function which we want to maximize.
```
plot(Lest(swedishpines), abs(iso - r) ~ r, main = "")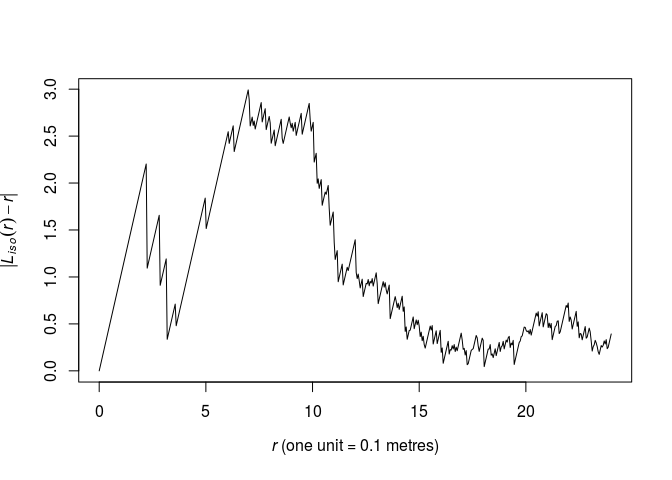
```
As seen from the plot, the maximum lies around (r = 6.5) by eye. We find the optimum explicitly like follows:
```
discrep <- function(r) {
  return(abs(as.function(Lest(swedishpines))(r) - r))
}
res <- optimise(discrep, interval = c(0.1, 20), maximum = TRUE)
print(res)
```
```
## $maximum
## [1] 6.984333
## 
## $objective
## [1] 2.992058
```
```
R <- res$maximum
```
This corresponds nicely with the plot.
Fit the stationary Strauss model with the chosen interaction distance using
```
ppm(swedishpines ~ 1, Strauss(R))
```
where R is your chosen value.
Interpret the printout: how strong is the interaction?
Plot the fitted pairwise interaction function using plot(fitin(fit)).

As we have assigned R, we simply write:
```
fit <- ppm(swedishpines ~ 1, Strauss(R))
print(fit)
```
```
## Stationary Strauss process
## 
## First order term:  beta = 0.0281221
## 
## Interaction distance:    6.984333
## Fitted interaction parameter gamma:   0.1434456
## 
## Relevant coefficients:
## Interaction 
##   -1.941799 
## 
## For standard errors, type coef(summary(x))
```
As seen, the (\gamma = 0.14) parameter is quite small. Thus there seems to be a strong negative association between points within distance R of each other. A (\gamma) of (0) implies the hard core process whereas (\gamma = 1) implies the Poisson process and thus CSR.

The pairwise interaction function become:
```
plot(fitin(fit))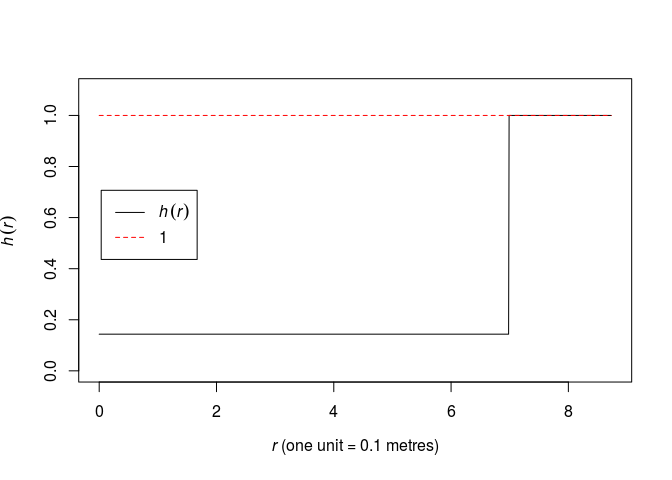
```

Exercise 2

In Question 1 we guesstimated the Strauss interaction distance parameter. Alternatively this parameter could be estimated by profile pseudolikelihood.

Look again at the plot of the (L)-function of swedishpines and determine a plausible range of possible values for the interaction distance.
```
plot(Lest(swedishpines), main = "")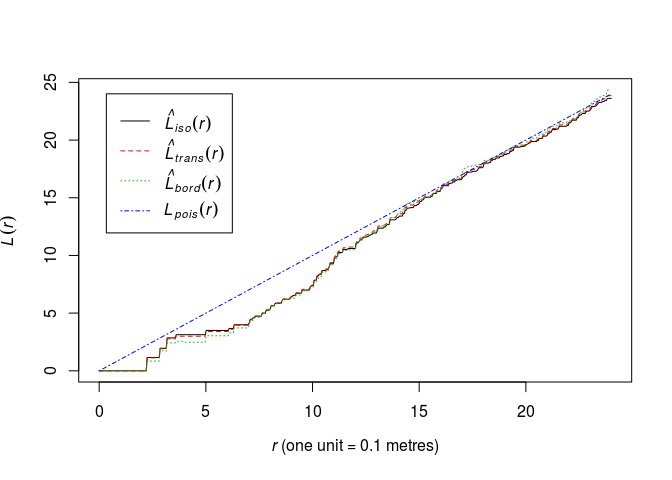
```
A conservative range of plausible interaction distances seems to be 3 to 15 meters.
Generate a sequence of values equally spaced across this range, for example, if your range of plausible values was ([0.05, 0.3]), then type
```
rvals <- seq(0.05, 0.3, by=0.01)
```
We generate the numbers between 3 and 12.
```
rvals <- seq(3, 12, by = 0.1)
```
Construct a data frame, with one column named r (matching the argument name of Strauss), containing these values. For example
```
D <- data.frame(r = rvals)
```
OK,
```
D <- data.frame(r = rvals)
```

Execute

fitp <- profilepl(D, Strauss, swedishpines ~ 1)

to find the maximum profile pseudolikelihood fit.

OK, let’s execute it:

fitp <- profilepl(D, Strauss, swedishpines ~ 1)

## (computing rbord)

## comparing 91 models...

## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38,
## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76,
## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90,  91.

## fitting optimal model...

## done.

Print and plot the object fitp.

print(fitp)

## profile log pseudolikelihood
## for model:  ppm(swedishpines ~ 1,  interaction = Strauss)
## fitted with rbord = 12
## interaction: Strauss process
## irregular parameter: r in [3, 12]
## optimum value of irregular parameter:  r = 9.8

plot(fitp)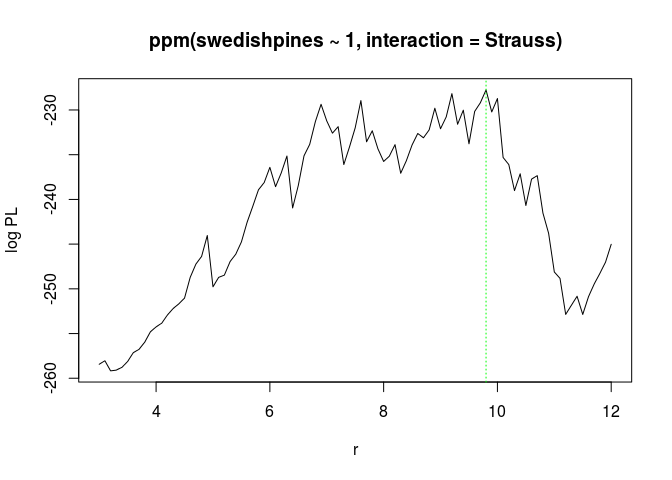

Compare the computed estimate of interaction distance (r) with your guesstimate. Compare the corresponding estimates of the Strauss interaction parameter (\gamma).
```
(Ropt <- reach(as.ppm(fitp)))
```
```
## [1] 9.8
```
The (r = 9.8) is not totally inconsistent with the previous estimate of (7).
Extract the fitted Gibbs point process model from the object fitp as
```
bestfit <- as.ppm(fitp)
```
OK, let’s do that:
```
bestfit <- as.ppm(fitp)
```

Exercise 3

For the Strauss model fitted in Question 1,

Generate and plot a simulated realisation of the fitted model using simulate.
```
s <- simulate(fit, drop = TRUE)
plot(s, main = "")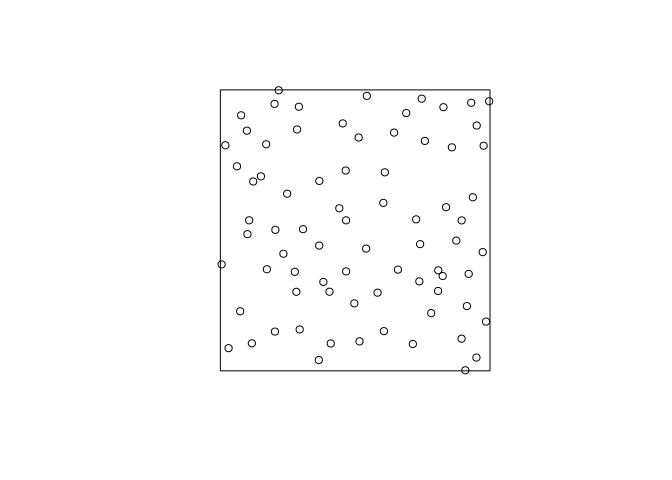
```

Plot the (L)-function of the data along with the global simulation envelopes from 19 realisations of the fitted model.

plot(envelope(fit, Lest, global = TRUE, nsim = 19, nsim2 = 100), main = "")

## Generating 119 simulated realisations of fitted Gibbs model (100 to 
## estimate the mean and 19 to calculate envelopes) ...
## 1, 2, 3, 4.6.8.10.12.14.16.18.20.22.24.26.28.30.32.34.36.38.
## 40.42.44.46.48.50.52.54.56.58.60.62.64.66.68.70.72.74.76.78
## .80.82.84.86.88.90.92.94.96.98.100.102.104.106.108.110.112.114.116.
## 118 119.
## 
## Done.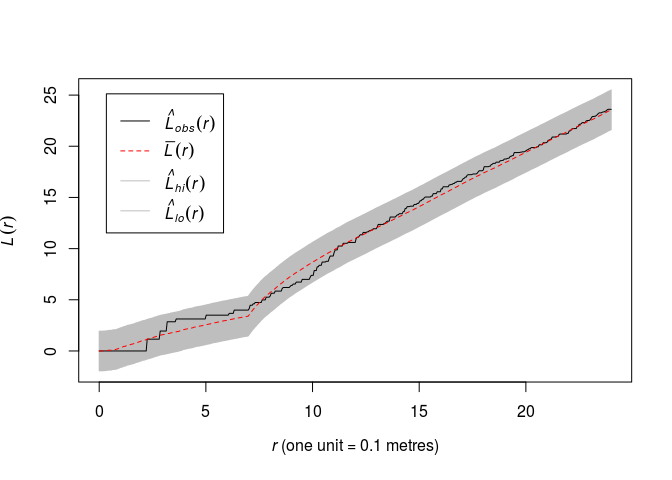

Exercise 4

Read the help file for Geyer.

See help(Geyer)

Fit a stationary Geyer saturation process to swedishpines, with the same interaction distance as for the Strauss model computed in Question 2, and trying different values of the saturation parameter sat = 1, 2, 3 say.

ppm(swedishpines ~ 1, Geyer(r = Ropt, sat = 1))

## Stationary Geyer saturation process
## 
## First order term:  beta = 0.07472669
## 
## Interaction distance:    9.8
## Saturation parameter:    1
## Fitted interaction parameter gamma:   0.1871555
## 
## Relevant coefficients:
## Interaction 
##   -1.675815 
## 
## For standard errors, type coef(summary(x))

ppm(swedishpines ~ 1, Geyer(r = Ropt, sat = 2))

## Stationary Geyer saturation process
## 
## First order term:  beta = 0.04707047
## 
## Interaction distance:    9.8
## Saturation parameter:    2
## Fitted interaction parameter gamma:   0.5242884
## 
## Relevant coefficients:
## Interaction 
##  -0.6457134 
## 
## For standard errors, type coef(summary(x))

ppm(swedishpines ~ 1, Geyer(r = Ropt, sat = 3))

## Stationary Geyer saturation process
## 
## First order term:  beta = 0.07603509
## 
## Interaction distance:    9.8
## Saturation parameter:    3
## Fitted interaction parameter gamma:   0.5261429
## 
## Relevant coefficients:
## Interaction 
##  -0.6421823 
## 
## For standard errors, type coef(summary(x))

Fit the same model with the addition of a log-quadratic trend.

gfit <- ppm(swedishpines ~ polynom(x, y, 2), Geyer(r = Ropt, sat = 3))

Plot the fitted trend and conditional intensity.

Here we use the log scale to be able to see the discs in the conditional intensity.
```
par(mfrow=c(1,2))
plot(gfit, log = TRUE, pause = FALSE)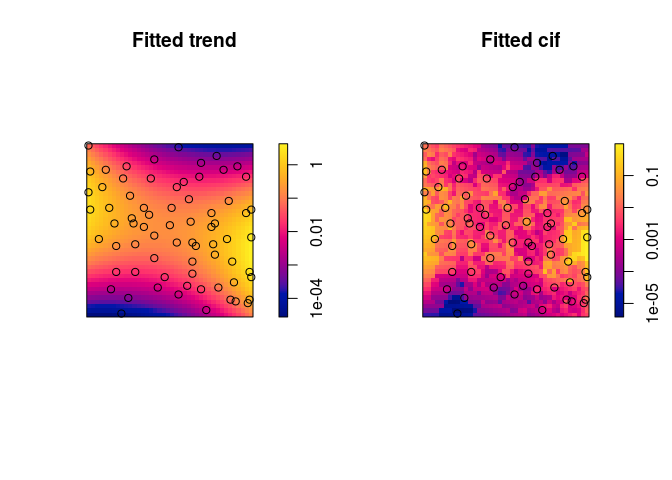
```

Exercise 5

Modify question 1 by using the Huang-Ogata approximate maximum likelihood algorithm (method="ho") instead of maximum pseudolikelihood (the default, method="mpl").

fit.mpl <- ppm(swedishpines ~ 1, Strauss(R), method = "mpl")
fit.ho  <- ppm(swedishpines ~ 1, Strauss(R), method = "ho")

## Simulating... 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38,
## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76,
## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99,  100.
## Done.

print(fit.ho)

## Stationary Strauss process
## 
## First order term:  beta = 0.03114674
## 
## Interaction distance:    6.984333
## Fitted interaction parameter gamma:   0.139353
## 
## Relevant coefficients:
## Interaction 
##   -1.970745 
## 
## For standard errors, type coef(summary(x))

print(fit.mpl)

## Stationary Strauss process
## 
## First order term:  beta = 0.0281221
## 
## Interaction distance:    6.984333
## Fitted interaction parameter gamma:   0.1434456
## 
## Relevant coefficients:
## Interaction 
##   -1.941799 
## 
## For standard errors, type coef(summary(x))

The fits are very similar.

Exercise 6

Repeat Question 2 for the inhomogeneous Strauss process with log-quadratic trend. The corresponding call to profilepl is

fitp <- profilepl(D, Strauss, swedishpines ~ polynom(x,y,2))

fitp2 <- profilepl(D, Strauss, swedishpines ~ polynom(x,y,2))

## (computing rbord)

## comparing 91 models...

## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38,
## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76,
## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90,  91.

## fitting optimal model...

## done.

print(fitp)

## profile log pseudolikelihood
## for model:  ppm(swedishpines ~ 1,  interaction = Strauss)
## fitted with rbord = 12
## interaction: Strauss process
## irregular parameter: r in [3, 12]
## optimum value of irregular parameter:  r = 9.8

print(fitp2)

## profile log pseudolikelihood
## for model:  ppm(swedishpines ~ polynom(x,  y,  2),  interaction = Strauss)
## fitted with rbord = 12
## interaction: Strauss process
## irregular parameter: r in [3, 12]
## optimum value of irregular parameter:  r = 9.8

Exercise 7

Repeat Question 3 for the inhomogeneous Strauss process with log-quadratic trend, using the inhomogeneous (L)-function Linhom in place of the usual (L)-function.

fit2 <- as.ppm(fitp2)
plot(envelope(fit2, Linhom, global = TRUE, nsim = 19, nsim2 = 100), main = "")

## Generating 119 simulated realisations of fitted Gibbs model (100 to 
## estimate the mean and 19 to calculate envelopes) ...
## 1, 2, 3, 4.6.8.10.12.14.16.18.20.22.24.26.28.30.32.34.36.38.
## 40.42.44.46.48.50.52.54.56.58.60.62.64.66.68.70.72.74.76.78
## .80.82.84.86.88.90.92.94.96.98.100.102.104.106.108.110.112.114.116.
## 118 119.
## 
## Done.

This site is open source. Improve this page.