Melb2018

Lab 8: Spacing and distances

This session is concerned with summary statistics for spacings and interpoint distances. The lecturer’s R script is available here (right click and save).

library(spatstat)

## Loading required package: spatstat.data

## Loading required package: methods

## Loading required package: nlme

## Loading required package: rpart

## 
## spatstat 1.56-1.007       (nickname: 'Damn You Autocorrect') 
## For an introduction to spatstat, type 'beginner'

Exercise 1

For the swedishpines data:

1. Calculate the estimate of the nearest neighbour distance distribution function (G) using Gest.

   G <- Gest(swedishpines)
   

2. Plot the estimate of (G(r)) against (r)

   plot(G, cbind(km, rs, han) ~ r, main = "Nearest neighbor distance distribution")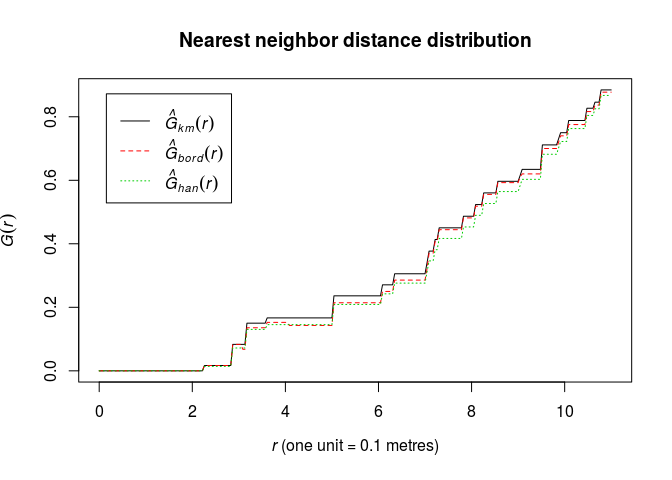
   

   

3. Plot the estimate of (G(r)) against the theoretical (Poisson) value (G_{\mbox{pois}}(r) = 1 - \exp(-\lambda \pi r^2)).

   E.g.

   plot(G, . ~ theo, main = "Nearest neighbor distribution")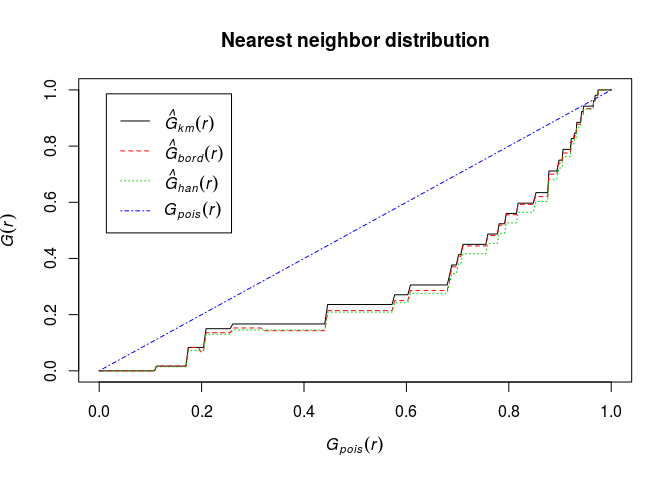
   

   

4. Define Fisher’s variance-stabilising transformation for c.d.f.’s by

   Phi <- function(x) asin(sqrt(x))
   

   Plot the (G) function using the formula Phi(.) ~ Phi(theo) and interpret it.

   Phi <- function(x) asin(sqrt(x))
   plot(G, Phi(.) ~ Phi(theo), main = "Nearest neighbor distribution")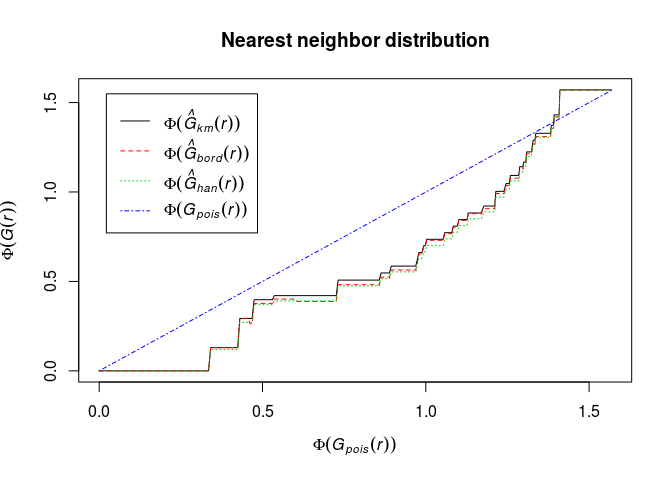
   

   

   The transformation has made the deviations from CSR in the central part of the curve smaller. We need envelopes to say anything about significance.

Exercise 2

For the swedishpines data:

1. Calculate the estimate of the nearest neighbour distance distribution function (F) using Fest.

   Fhat <- Fest(swedishpines)
   

2. Plot the estimate of (F(r)) against (r)

   plot(Fhat, main = "Empty Space function")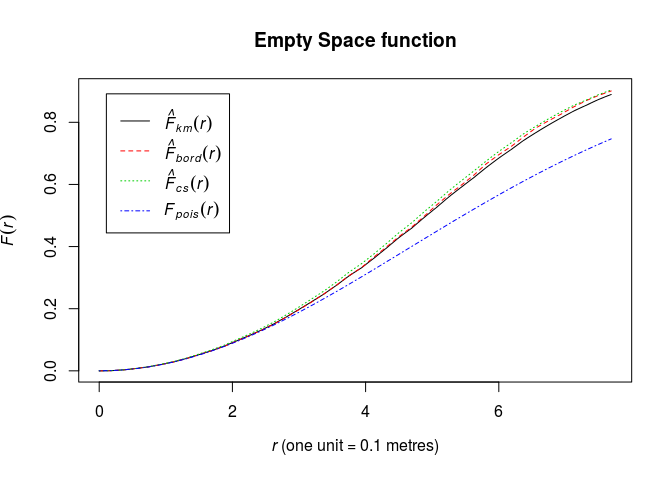
   

   

3. Plot the estimate of (F(r)) against the theoretical (Poisson) value (F_{\mbox{pois}}(r) = 1 - \exp(-\lambda \pi r^2)).

   plot(Fhat, . ~ theo, main = "")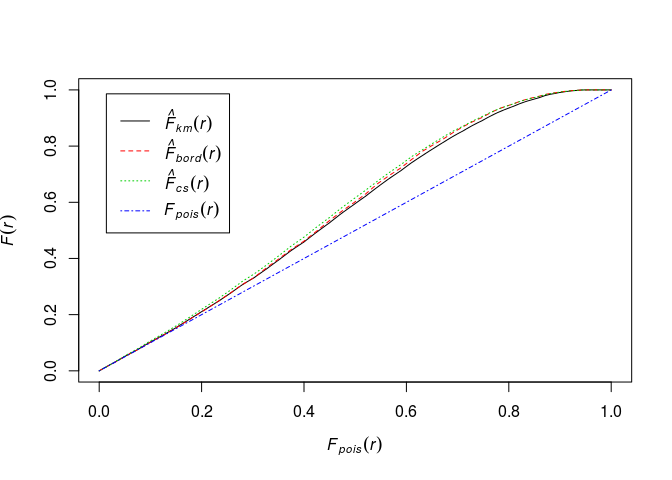
   

   

4. Define Fisher’s variance-stabilising transformation for c.d.f.’s by

   Phi <- function(x) asin(sqrt(x))
   

   Plot the (F) function using the formula Phi(.) ~ Phi(theo) and interpret it.

   Phi <- function(x) asin(sqrt(x))
   plot(Fhat, Phi(.) ~ Phi(theo), main = "")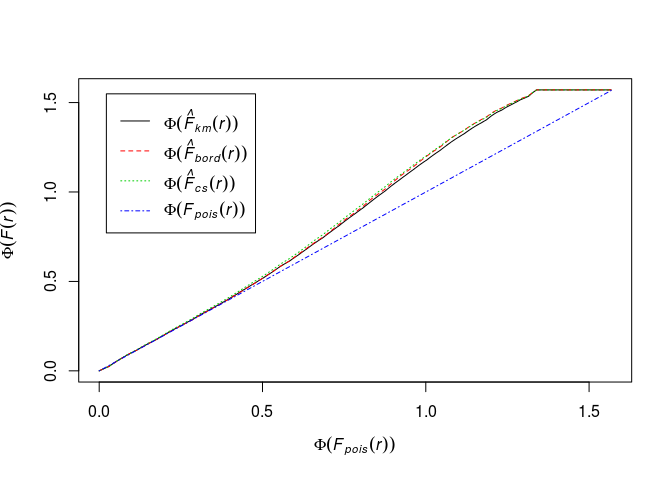
   

   

   The transformation has changed the picture much. It looks like deviation from CSR, but again, without envelopes it’s hard to draw conclusions.

This site is open source. Improve this page.