Melb2018
Lab 7: Envelopes and Monte Carlo tests
This session is concerned with evelopes of summary statistics and Monte Carlo tests. The lecturer’s R script is available here (right click and save).
library(spatstat)
## Loading required package: spatstat.data
## Loading required package: methods
## Loading required package: nlme
## Loading required package: rpart
##
## spatstat 1.56-1.007 (nickname: 'Damn You Autocorrect')
## For an introduction to spatstat, type 'beginner'
Exercise 1
For the swedishpines data:
-
Plot the (K) function along with pointwise envelopes from 39 simulations of CSR:
plot(envelope(swedishpines, Kest, nsim=39))OK,
plot(envelope(swedishpines, Kest, nsim=39), main = "")## Generating 39 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, ## 39. ## ## Done.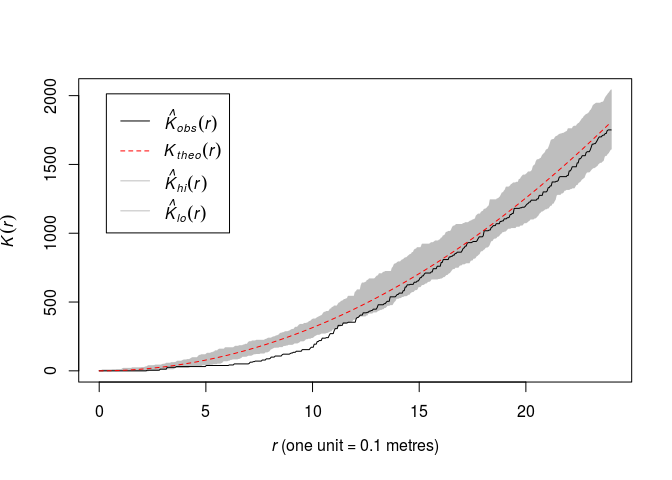
-
Plot the (L) function along with pointwise envelopes from 39 simulations of CSR.
Like above now with
Lest:plot(envelope(swedishpines, Lest, nsim=39), main = "")## Generating 39 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, ## 39. ## ## Done.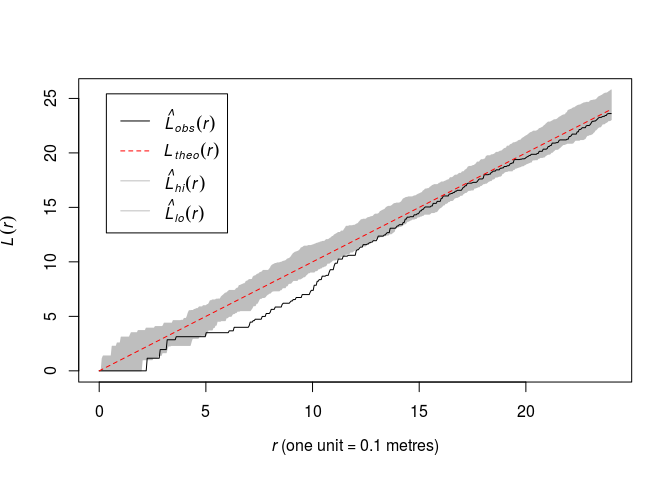
-
Plot the (L) function along with simultaneous envelopes from 19 simulations of CSR, using
ginterval=c(0,5).plot(envelope(swedishpines, Lest, nsim = 19, global = TRUE, ginterval=c(0,5)), main = "")## Generating 19 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19. ## ## Done.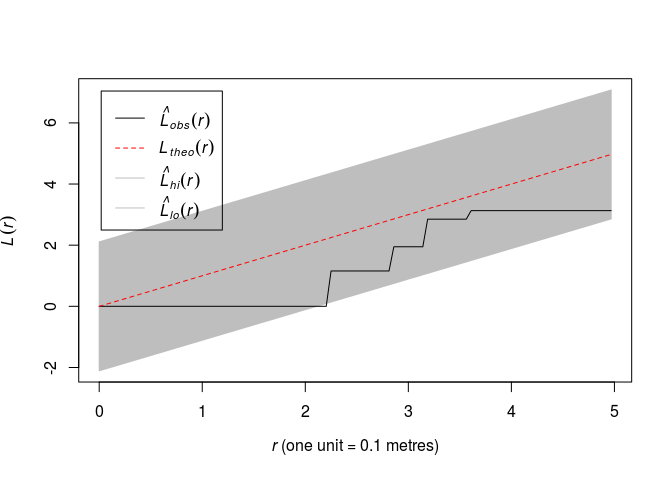
-
Plot the (L) function for along with simultaneous envelopes from 99 simulations of CSR using
ginterval=c(0,5). What is the significance level of the associated test?plot(envelope(swedishpines, Lest, nsim = 99, global = TRUE, ginterval=c(0,5)), main = "")## Generating 99 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, ## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, ## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99. ## ## Done.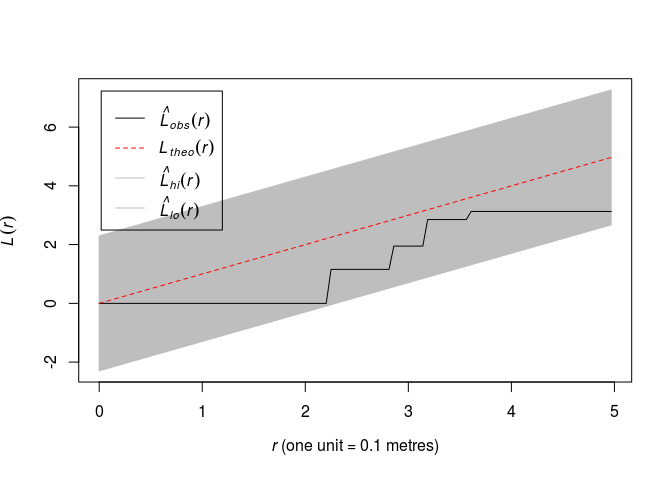
Which yields an 1% significance test.
Exercise 2
To understand the difficulties with the (K)-function when the point pattern is not spatially homogeneous, try the following experiment (like in the previous lab session).
-
Generate a simulated realisation of an inhomogeneous Poisson process, e.g.
X <- rpoispp(function(x,y){ 200 * exp(-3 * x) })OK,
X <- rpoispp(function(x,y){ 200 * exp(-3 * x) }) -
Compute simulation envelopes (of your favorite type) of the (K)- or (L)-function under CSR. They may well indicate significant departure from CSR.
There indeed often seems to be a departure from CSR:
par(mfrow=c(1,2)) plot(envelope(X, Kest, global = TRUE))## Generating 99 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, ## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, ## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99. ## ## Done.plot(envelope(X, Lest, global = TRUE))## Generating 99 simulations of CSR ... ## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, ## 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, ## 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99. ## ## Done.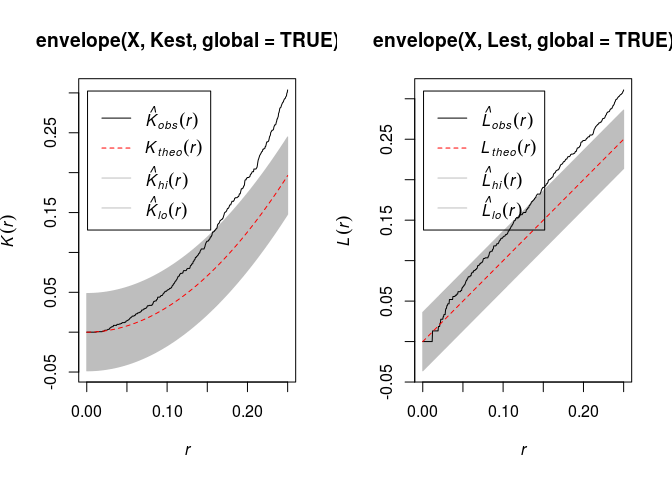
-
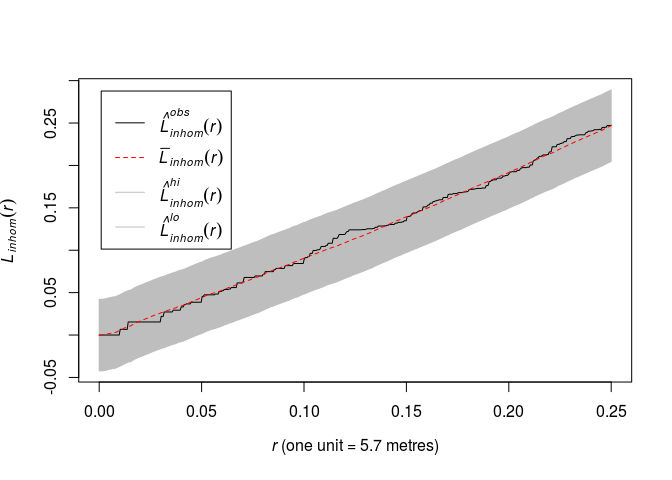
Fit a Poisson point process model to the
japanesepinesdata with log-quadratic trend (formula~polynom(x,y,2)). Plot the (L)-function of the data along with simultaneous envelopes from 99 simulations of the fitted model.This can be done by the code:
fit <- ppm(japanesepines ~ polynom(x, y, 2)) plot(envelope(fit, Linhom, global = TRUE), main = "")## Generating 198 simulated realisations of fitted Poisson model (99 to ## estimate the mean and 99 to calculate envelopes) ... ## 1, 2, 3, 4.6.8.10.12.14.16.18.20.22.24.26.28.30.32.34.36.38. ## 40.42.44.46.48.50.52.54.56.58.60.62.64.66.68.70.72.74.76.78 ## .80.82.84.86.88.90.92.94.96.98.100.102.104.106.108.110.112.114.116. ## 118.120.122.124.126.128.130.132.134.136.138.140.142.144.146.148.150.152.154.156 ## .158.160.162.164.166.168.170.172.174.176.178.180.182.184.186.188.190.192.194. ## 196. 198. ## ## Done.