ECAS2019

Lab 2: Intensity – solutions

This session covers exploratory tools and formal model-fitting procedures for investigating intensity.

library(spatstat)

Exercise 1

The dataset japanesepines contains the locations of Japanese Black Pine trees in a study region.

Plot the japanesepines data.

We use the generic plot function which is dispatched to plot.ppp:
```
plot(japanesepines)
```
What is the average intensity (the average number of points per unit area?

The average intensity can be computed via intensity.ppp:
```
intensity(japanesepines)
```
```
## [1] 65
```
Using density.ppp, compute a kernel estimate of the spatially-varying intensity function for the Japanese pines data, using a Gaussian kernel with standard deviation $\sigma=0.1$ units, and store the estimated intensity in an object D say.

From the documentation (?density.ppp) we see that the following will work:
```
D <- density(japanesepines, sigma = 0.1)
```
Plot a colour image of the kernel estimate D.

The plotting of the colour image is automatically done by dispatched call to the plot.im method by calling plot on the im object.
```
plot(D, main = "")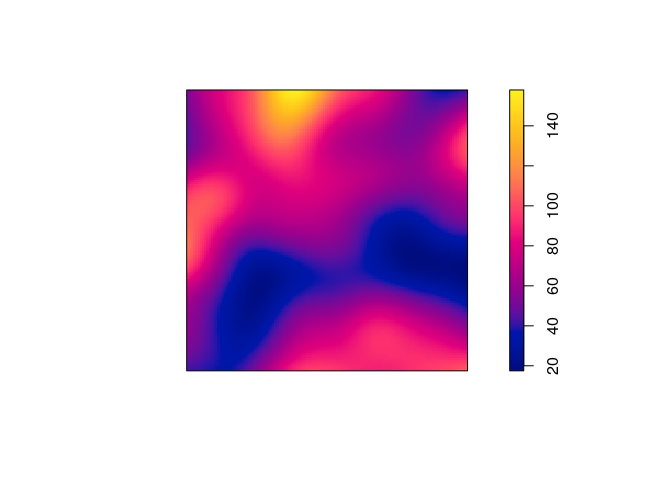
```
Most plotting commands will accept the argument add=TRUE and interpret it to mean that the plot should be drawn over the existing display, without clearing the screen beforehand. Use this to plot a colour image of the kernel estimate D with the original Japanese Pines data superimposed.

We can use the add = TRUE functionality of the plotting methods.
```
plot(D, main = "")
plot(japanesepines, add = TRUE, cols = "white", cex = 0.5, pch = 16)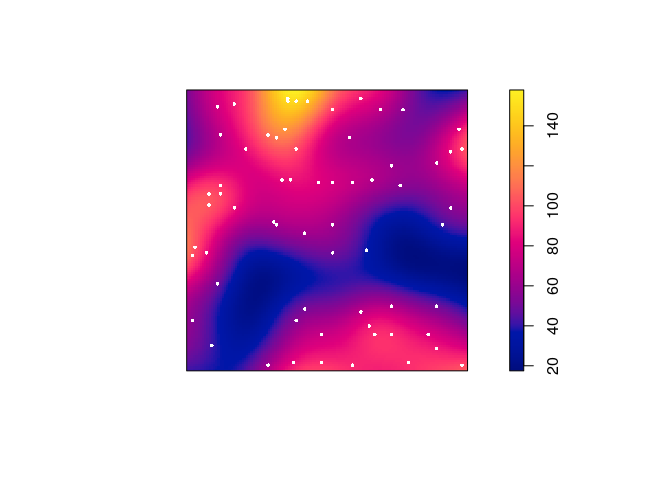
```
Plot the kernel estimate without the ‘colour ribbon’.

From help("plot.im") we see that ribbon = FALSE disables the colour key:
```
plot(D, main = "", ribbon = FALSE)
plot(japanesepines, add = TRUE, cols = "white", cex = 0.5, pch = 16)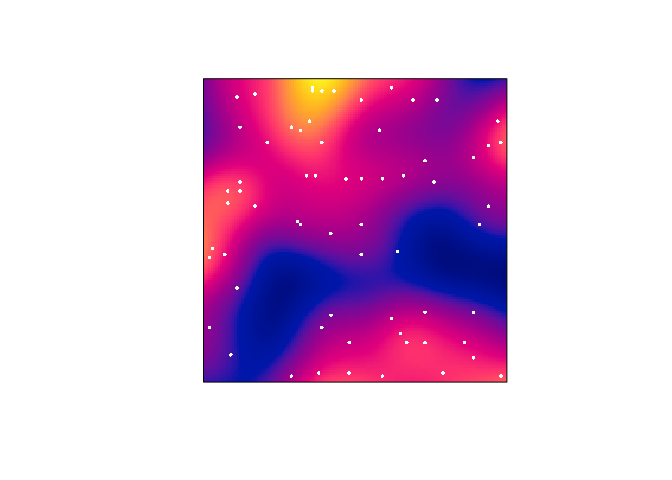
```
Try the following command
```
persp(D, theta=70, phi=25, shade=0.4)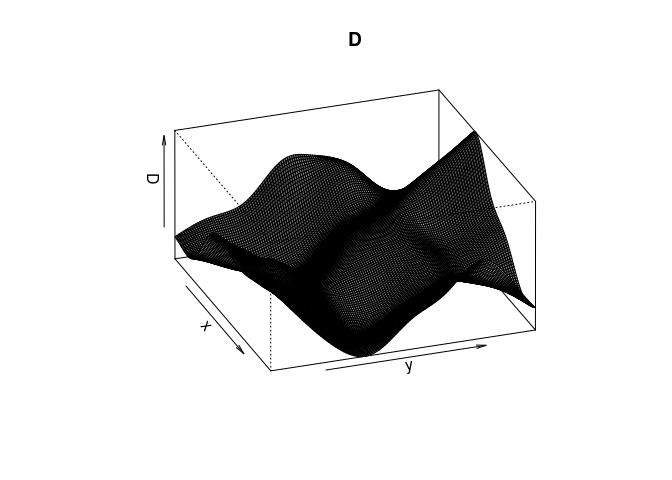
```
and find the documentation for the arguments theta, phi and shade.

It dispatches to persp.im, but these arguments are then passed down to persp.default through the dots (...). From the documentation of persp.default they are “angles defining the viewing direction. theta gives the azimuthal direction and phi the colatitude.” The shade controls the shading of the surface facets.
```
persp(D, theta=70, phi=25, shade=0.4, main = "")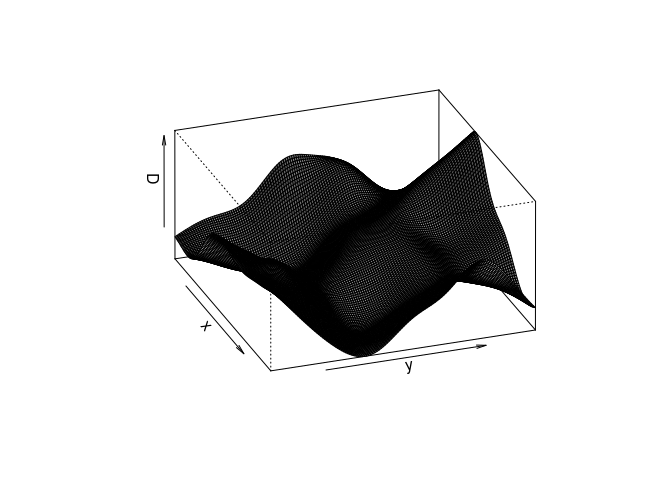
```
Find the maximum and minimum values of the intensity estimate over the study region. (Hint: Use summary or range)
```
range(D)
```
```
## [1]  17.47221 157.95229
```
The kernel estimate of intensity is defined so that its integral over the entire study region is equal to the number of points in the data pattern, ignoring edge effects. Check whether this is approximately true in this example. (Hint: use integral)

Calling integral.im we see that the integral is close to the observed number of points 65:
```
round(integral(D))
```
```
## [1] 64
```

Exercise 2

The bei dataset gives the locations of trees in a survey area with additional covariate information in a list bei.extra.

Assign the elevation covariate to a variable elev by typing
```
elev <- bei.extra$elev
```
Plot the trees on top of an image of the elevation covariate.
```
plot(elev)
plot(bei, add = TRUE, col = "black")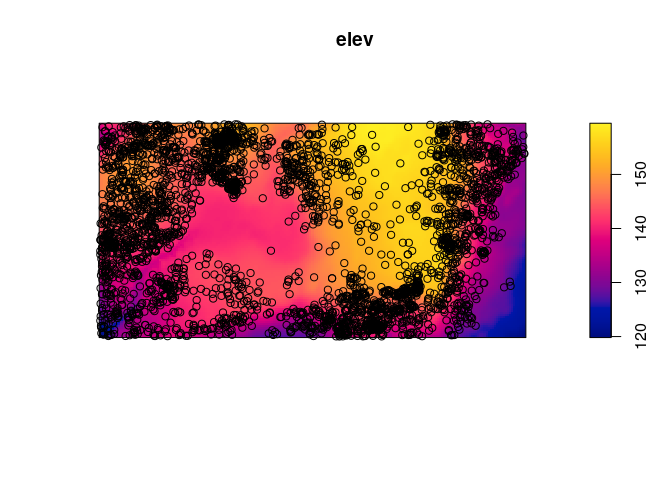
```
Assume that the intensity of trees is a function $\lambda(u) = \rho(e(u))$ where $e(u)$ is the terrain elevation at location u. Compute a nonparametric estimate of the function $\rho$ and plot it by
```
rh <- rhohat(bei, elev)
plot(rh)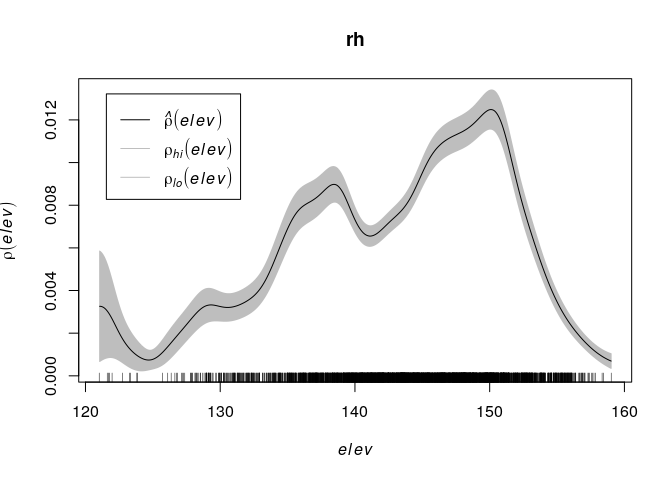
```

Compute the predicted intensity based on this estimate of $\rho$ .

prh <- predict(rh)
plot(prh, main = "")
plot(bei, add = TRUE, cols = "white", cex = .2, pch = 16)

Compute a non-parametric estimate of intensity by kernel smoothing, and compare with the predicted intensity above.

The kernel density estimate of the points is computed and plotted with the following code:
```
dbei <- density(bei, sigma = bw.scott)
plot(dbei, main = "")
plot(bei, add = TRUE, cols = "white", cex = .2, pch = 16)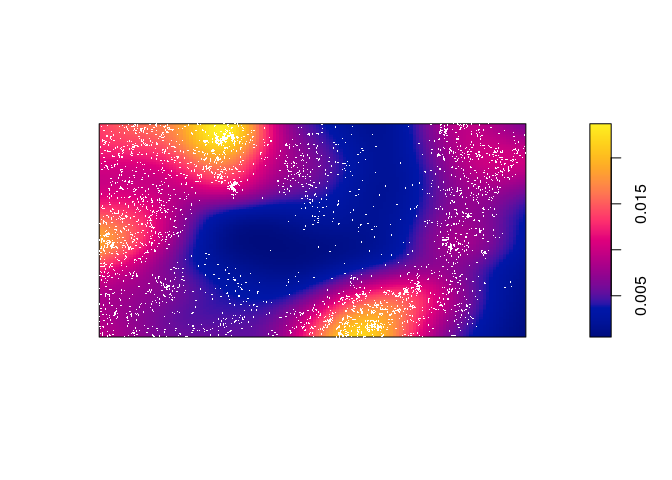
```
Which seems to be quite different form the predicted intentisty.

Bonus info: To plot the two intensity estimates next to each other you collect the estimates as a spatial object list (solist) and plot the result (the estimates are called pred and ker below):

l <- solist(pred, ker)
plot(l, equal.ribbon = TRUE, main = "", 
     main.panel = c("rhohat prediction", "kernel smoothing"))

l <- solist(prh, dbei)
plot(l, equal.ribbon = TRUE, main = "",
     main.panel = c("rhohat prediction", "kernel smoothing"))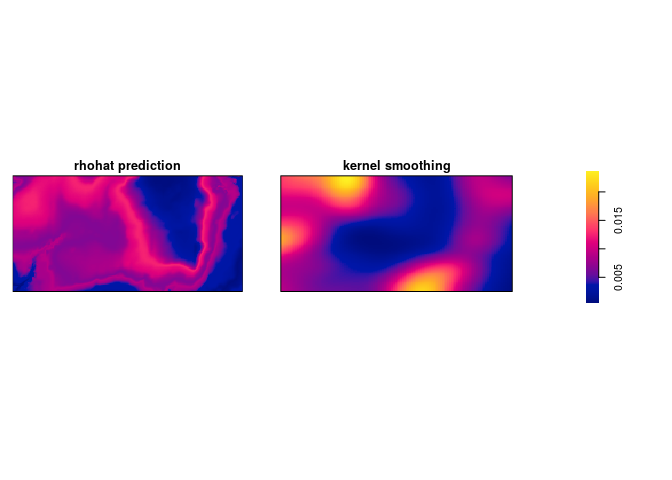

Exercise 3

The command rpoispp(100) generates realisations of the Poisson process with intensity $\lambda = 100$ in the unit square.

Repeat the command plot(rpoispp(100)) several times to build your intuition about the appearance of a completely random pattern of points.

Let’s plot it three times:
```
replicate(3, plot(rpoispp(lambda = 100), main = ""))
```
As can be seen, the points (unsurprisingly) are much more random that want one might think. “Randomly” drawing points on a piece of paper one would usually draw a point pattern that is more regular (i.e. the points are repulsive).
Try the same thing with intensity $\lambda = 1.5$ .

For brevity we only do it once here:
```
plot(rpoispp(lambda = 1.5), main = "")
```
Here we expect 1.5 points in the plot each time.

Exercise 4

Returning to the Japanese Pines data,

Fit the uniform Poisson point process model to the Japanese Pines data

ppm(japanesepines~1)

We fit the Poisson process model with the given command and print the output:

m.jp <- ppm(japanesepines ~ 1)
print(m.jp)

## Stationary Poisson process
## Intensity: 65
##             Estimate      S.E.  CI95.lo  CI95.hi Ztest     Zval
## log(lambda) 4.174387 0.1240347 3.931284 4.417491   *** 33.65499

Read off the fitted intensity. Check that this is the correct value of the maximum likelihood estimate of the intensity.

We extract the coeficient with the coef function, and compare to the straightforward estimate obtained by `intensity``:
```
unname(exp(coef(m.jp)))
```
```
## [1] 65
```
```
intensity(japanesepines)
```
```
## [1] 65
```
As seen, they agree exactly.

Exercise 5

The japanesepines dataset is believed to exhibit spatial inhomogeneity.

Plot a kernel smoothed intensity estimate.

Plot the kernel smoothed intensity estimate selecting the bandwidth with bw.scott:

jp.dens <- density(japanesepines, sigma = bw.scott)
plot(jp.dens)
plot(japanesepines, col = "white", cex = .4, pch = 16, add = TRUE)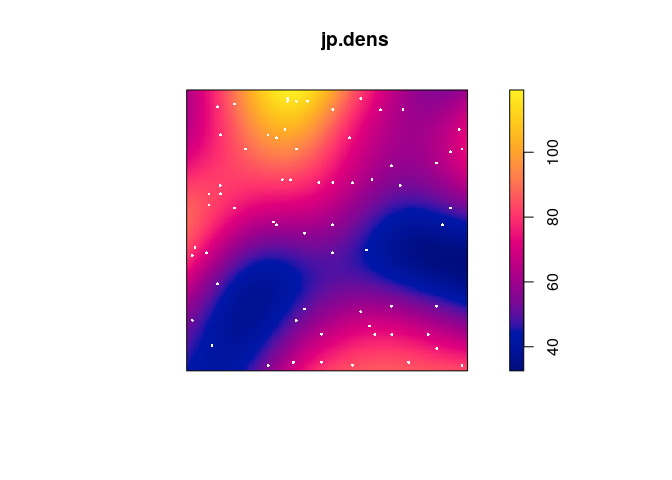

Fit the Poisson point process models with loglinear intensity (trend formula ~x+y) and log-quadratic intensity (trend formula ~polynom(x,y,2)) to the Japanese Pines data.

We fit the two models with ppm:
```
jp.m <- ppm(japanesepines ~ x + y)
jp.m2 <- ppm(japanesepines ~ polynom(x, y, 2) )
```

extract the fitted coefficients for these models using coef.

coef(jp.m)

## (Intercept)           x           y 
##   4.0670790  -0.2349641   0.4296171

coef(jp.m2)

## (Intercept)           x           y      I(x^2)    I(x * y)      I(y^2) 
##   4.0645501   1.1436854  -1.5613621  -0.7490094  -1.2009245   2.5061569

Plot the fitted model intensity (using plot(predict(fit)))

par(mar=rep(0,4))
plot(predict(jp.m), main = "")

plot(predict(jp.m, se=TRUE)$se, main = "")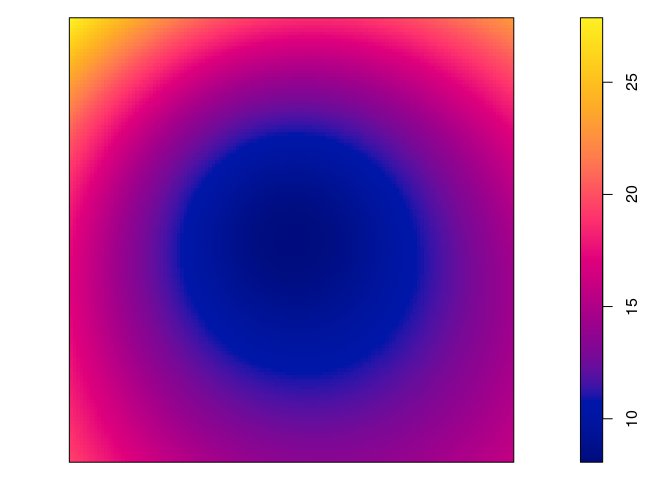

plot(predict(jp.m2), main = "")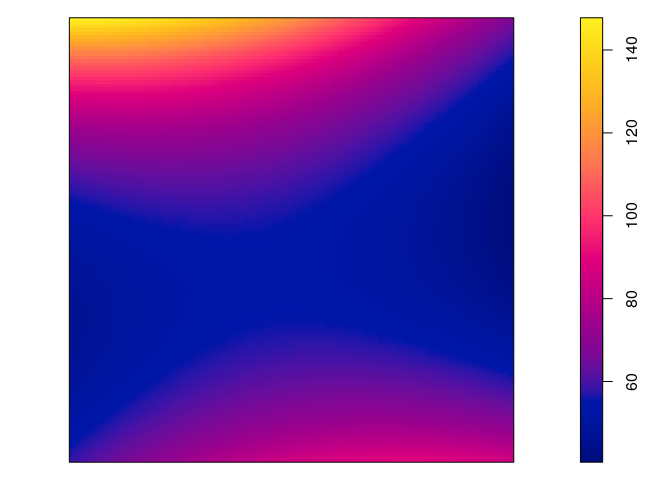

plot(predict(jp.m2, se=TRUE)$se, main = "")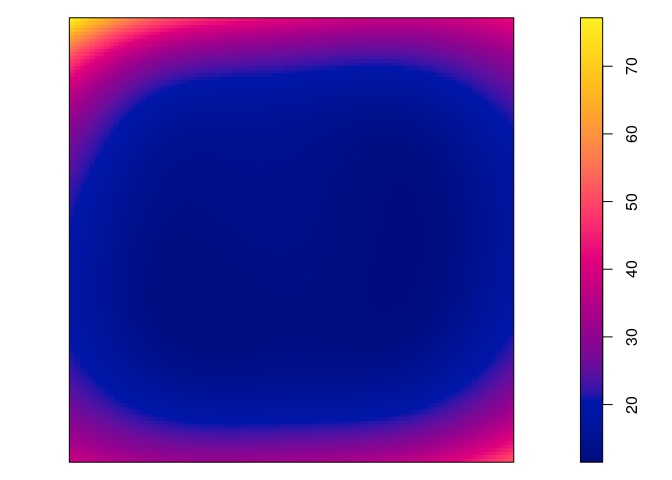

perform the Likelihood Ratio Test for the null hypothesis of a loglinear intensity against the alternative of a log-quadratic intensity, using anova.

anova(jp.m, jp.m2)

## Analysis of Deviance Table
## 
## Model 1: ~x + y   Poisson
## Model 2: ~x + y + I(x^2) + I(x * y) + I(y^2)      Poisson
##   Npar Df Deviance
## 1    3            
## 2    6  3   3.3851

Generate 10 simulated realisations of the fitted log-quadratic model, and plot them, using plot(simulate(fit, nsim=10)) where fit is the fitted model.
```
par(mar=rep(0.5,4))
plot(simulate(jp.m2, nsim=10), main = "")
```
```
## Generating 10 simulated patterns ...1, 2, 3, 4, 5, 6, 7, 8, 9,  10.
```

Exercise 6

The update command can be used to re-fit a point process model using a different model formula.

Type the following commands and interpret the results:

fit0 <- ppm(japanesepines ~ 1)
fit1 <- update(fit0, . ~ x)
fit1

## Nonstationary Poisson process
## 
## Log intensity:  ~x
## 
## Fitted trend coefficients:
## (Intercept)           x 
##   4.2895587  -0.2349362 
## 
##               Estimate      S.E.   CI95.lo   CI95.hi Ztest       Zval
## (Intercept)  4.2895587 0.2411952  3.816825 4.7622926   *** 17.7845936
## x           -0.2349362 0.4305416 -1.078782 0.6089098       -0.5456759

fit2 <- update(fit1, . ~ . + y)
fit2

## Nonstationary Poisson process
## 
## Log intensity:  ~x + y
## 
## Fitted trend coefficients:
## (Intercept)           x           y 
##   4.0670790  -0.2349641   0.4296171 
## 
##               Estimate      S.E.    CI95.lo   CI95.hi Ztest       Zval
## (Intercept)  4.0670790 0.3341802  3.4120978 4.7220602   *** 12.1703167
## x           -0.2349641 0.4305456 -1.0788181 0.6088898       -0.5457357
## y            0.4296171 0.4318102 -0.4167154 1.2759495        0.9949211

OK, let’s do that:

fit0 <- ppm(japanesepines ~ 1)
fit1 <- update(fit0, . ~ x)
fit1

## Nonstationary Poisson process
## 
## Log intensity:  ~x
## 
## Fitted trend coefficients:
## (Intercept)           x 
##   4.2895587  -0.2349362 
## 
##               Estimate      S.E.   CI95.lo   CI95.hi Ztest       Zval
## (Intercept)  4.2895587 0.2411952  3.816825 4.7622926   *** 17.7845936
## x           -0.2349362 0.4305416 -1.078782 0.6089098       -0.5456759

fit2 <- update(fit1, . ~ . + y)
fit2

## Nonstationary Poisson process
## 
## Log intensity:  ~x + y
## 
## Fitted trend coefficients:
## (Intercept)           x           y 
##   4.0670790  -0.2349641   0.4296171 
## 
##               Estimate      S.E.    CI95.lo   CI95.hi Ztest       Zval
## (Intercept)  4.0670790 0.3341802  3.4120978 4.7220602   *** 12.1703167
## x           -0.2349641 0.4305456 -1.0788181 0.6088898       -0.5457357
## y            0.4296171 0.4318102 -0.4167154 1.2759495        0.9949211

Now type step(fit2) and interpret the results.

The backwards selection is done with the code:

step(fit2)

## Start:  AIC=-407.96
## ~x + y
## 
##        Df     AIC
## - x     1 -409.66
## - y     1 -408.97
## <none>    -407.96
## 
## Step:  AIC=-409.66
## ~y
## 
##        Df     AIC
## - y     1 -410.67
## <none>    -409.66
## 
## Step:  AIC=-410.67
## ~1

## Stationary Poisson process
## Intensity: 65
##             Estimate      S.E.  CI95.lo  CI95.hi Ztest     Zval
## log(lambda) 4.174387 0.1240347 3.931284 4.417491   *** 33.65499

First, given two models the preferred model is the one with the minimum AIC value. In step 1, the removal of x results in the least AIC and is hence deleted. In step 2, removing y results in a lower AIC than not deleing anything and is thus deleted. This results in the constant model.

Exercise 7

The bei dataset gives the locations of trees in a survey area with additional covariate information in a list bei.extra.

Fit a Poisson point process model to the data which assumes that the intensity is a loglinear function of terrain slope and elevation (hint: use data = bei.extra in ppm).

We fit the log-linear intensity model with the following:
```
bei.m <- ppm(bei ~ elev + grad, data = bei.extra)
```
Read off the fitted coefficients and write down the fitted intensity function.

The coefficents are extraced with coef:
```
coef(bei.m)
```
```
## (Intercept)        elev        grad 
## -8.56355220  0.02143995  5.84646680
```
Hence the model is $log\lambda(u) = -8.55 + 0.02\cdot E(u) + 5.84 G(u)$ where $E(u)$ and $G(u)$ is the elevation and gradient, respectively, at $u$ .

Plot the fitted intensity as a colour image.

plot(predict(bei.m), main = "")
plot(bei, cex = 0.3, pch = 16, cols = "white", add = TRUE)

extract the estimated variance-covariance matrix of the coefficient estimates, using vcov.

We call vcov on the fitted model object:

vcov(bei.m)

##               (Intercept)          elev          grad
## (Intercept)  0.1163586583 -7.774771e-04 -0.0354792767
## elev        -0.0007774771  5.234331e-06  0.0001992266
## grad        -0.0354792767  1.992266e-04  0.0654239289

Compute and plot the standard error of the intensity estimate (see help(predict.ppm)).

From the documentation the argument se will trigger the computation of the standard errors. These are then plotted in the standard manner.
```
std.err <- predict(bei.m, se = TRUE)$se
plot(std.err, main = "")
```

Exercise 8

Fit Poisson point process models to the Japanese Pines data, with the following trend formulas. Read off an expression for the fitted intensity function in each case.

Trend formula	Fitted intensity function
`~1`	$\log\lambda(u) = 4.17$
`~x`	$\log\lambda(u) = 4.28 - 0.23x$
`~sin(x)`	$\log\lambda(u) = 4.29 - 0.26\sin(x)$
`~x+y`	$\log\lambda(u) = 4.07 - 0.23x + 0.42y$
`~polynom(x,y,2)`	$\log\lambda(u) = 4.06 + 1.14x - 1.56y - 0.75x^2 - 1.20xy + 2.51y^2$
`~factor(x < 0.4)`	$\log\lambda(u) = 4.10 + 0.16\cdot I(x < 0.4)$

(Here, $I(\cdot)$ denote the indicator function.)

The fitted intensity functions have been written into the table based on the follwing model fits:

coef(ppm1 <- ppm(japanesepines ~ 1)) 

## log(lambda) 
##    4.174387

coef(ppm2 <- ppm(japanesepines ~ x))

## (Intercept)           x 
##   4.2895587  -0.2349362

coef(ppm3 <- ppm(japanesepines ~ sin(x)))

## (Intercept)      sin(x) 
##   4.2915935  -0.2594537

coef(ppm4 <- ppm(japanesepines ~ x + y))

## (Intercept)           x           y 
##   4.0670790  -0.2349641   0.4296171

coef(ppm5 <- ppm(japanesepines ~ polynom(x, y, 2)))

## (Intercept)           x           y      I(x^2)    I(x * y)      I(y^2) 
##   4.0645501   1.1436854  -1.5613621  -0.7490094  -1.2009245   2.5061569

coef(ppm6 <- ppm(japanesepines ~ factor(x < 0.4)))

##         (Intercept) factor(x < 0.4)TRUE 
##           4.1048159           0.1632665

Exercise 9

Make image plots of the fitted intensities for the inhomogeneous models above.

Again, we use plot(predict()):

plot(predict(ppm1), main = "")

plot(predict(ppm2), main = "")

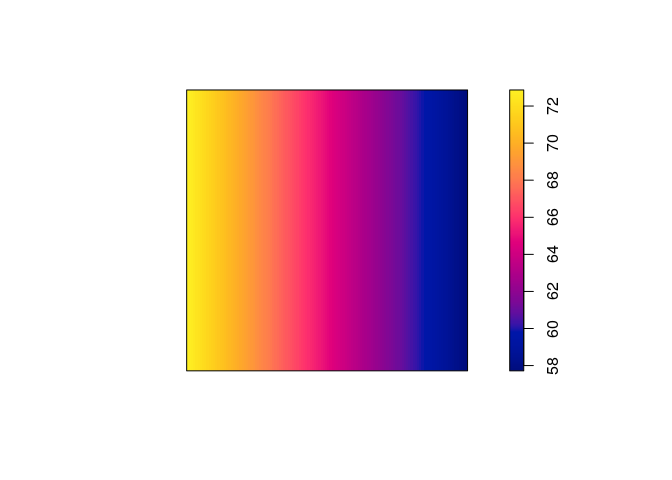
plot(predict(ppm3), main = "")

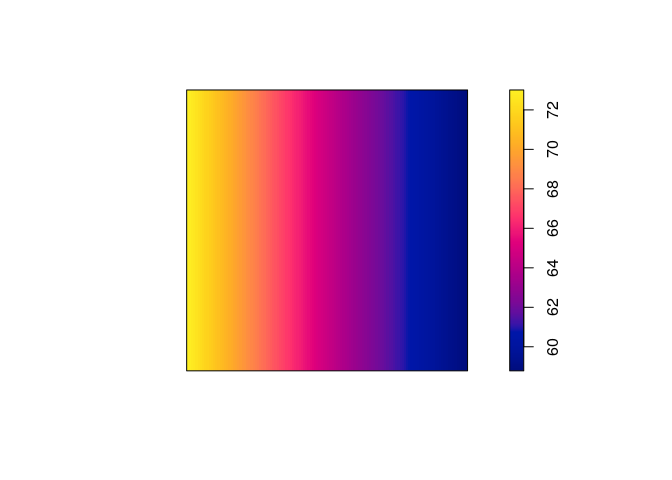
plot(predict(ppm4), main = "")

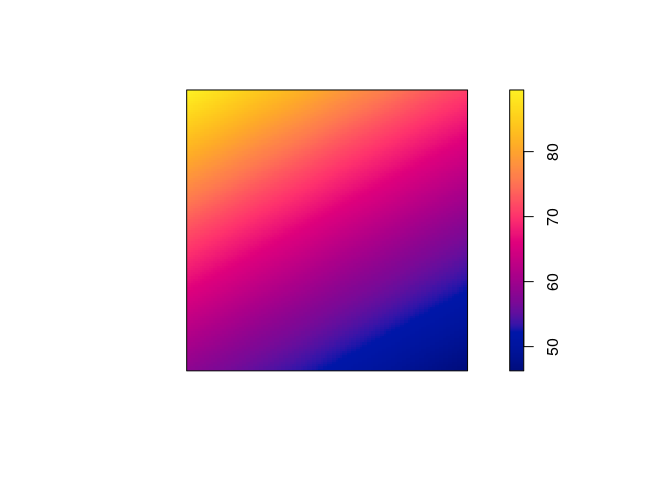
plot(predict(ppm5), main = "")

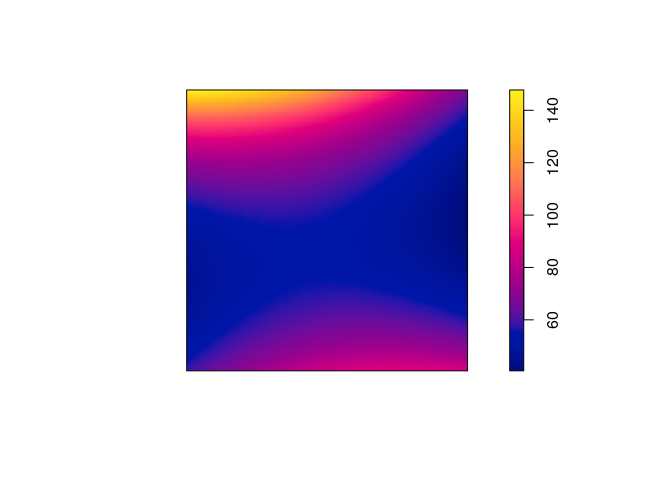
plot(predict(ppm6), main = "")

Exercise 10

The dataset hamster is a multitype pattern representing the locations of cells of two types, dividing and pyknotic.

plot the patterns of pyknotic and dividing cells separately;
```
plot(split(hamster), main = "")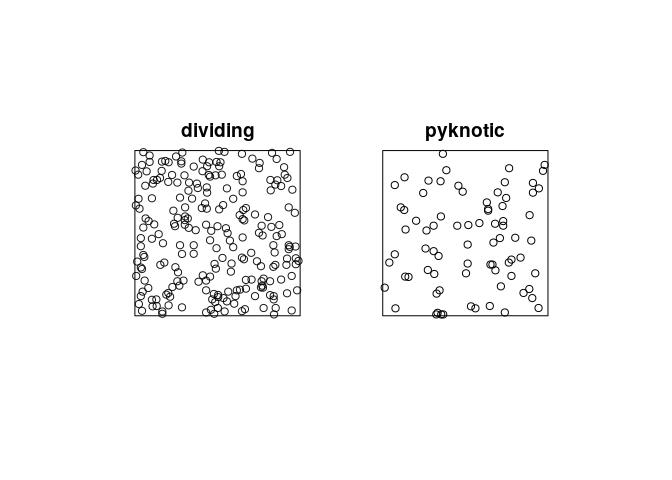
```
plot kernel estimates of the intensity functions of pyknotic and dividing cells separately;
```
plot(density(split(hamster)), main = "")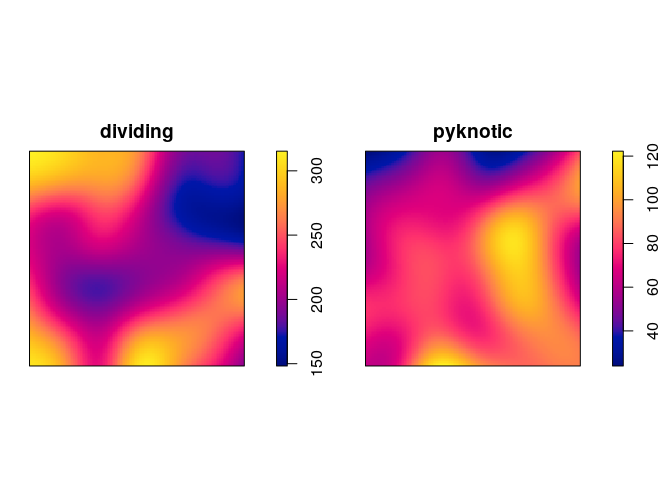
```
use relrisk to perform cross-validated bandwidth selection and computation of the relative intensity of pyknotic cells.
```
plot(relrisk(hamster, hmax = 1, relative = TRUE, control = "dividing"))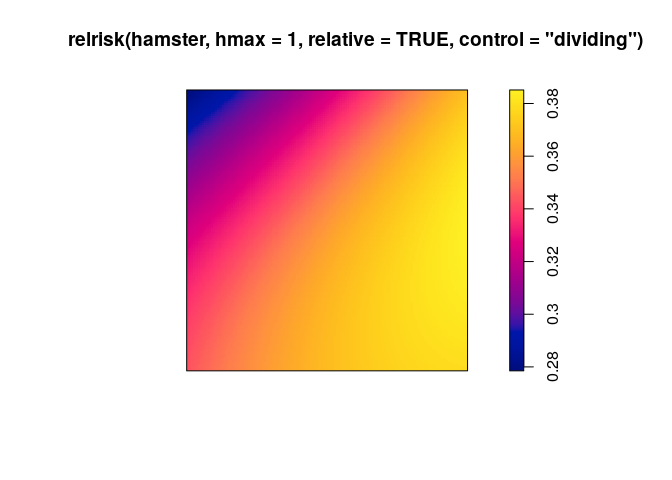
```

Exercise 11

The dataset ants is a multitype point pattern representing the locations of nests of two species of ants.

plot the data.
```
plot(ants)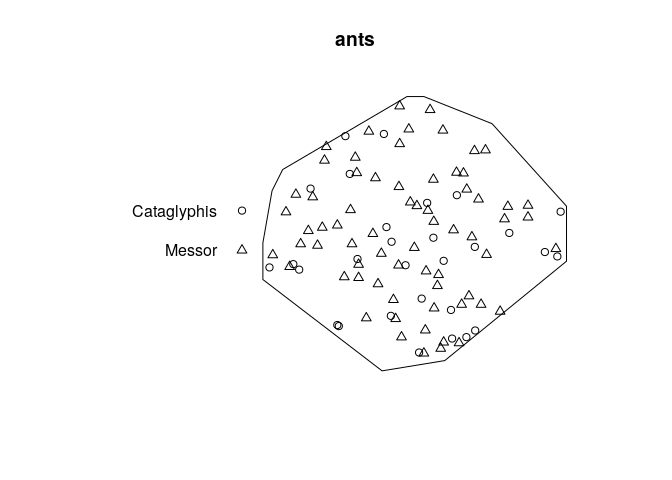
```

Fit the model ppm(ants ~ marks) and interpret the result. Compare the result with summary(ants) and explain the similarities.

fit1 <- ppm(ants ~ marks)

This is a Poisson model with a separate constant intensity for each mark. The fitted intensities are:

exp(coef(fit1)[1])

##  (Intercept) 
## 6.762949e-05

exp(coef(fit1)[1] + coef(fit1)[2])

##  (Intercept) 
## 0.0001585795

This agrees perfectly with the output of summary(ants):

summary(ants)

## Marked planar point pattern:  97 points
## Average intensity 0.0002261486 points per square unit (one unit = 0.5 feet)
## 
## Coordinates are integers
## i.e. rounded to the nearest unit (one unit = 0.5 feet)
## 
## Multitype:
##             frequency proportion    intensity
## Cataglyphis        29  0.2989691 6.761144e-05
## Messor             68  0.7010309 1.585372e-04
## 
## Window: polygonal boundary
## single connected closed polygon with 11 vertices
## enclosing rectangle: [-25, 803] x [-49, 717] units
## Window area = 428922 square units
## Unit of length: 0.5 feet
## Fraction of frame area: 0.676

Fit the model ppm(ants ~ marks + x) and write down an expression for the fitted intensity function.
```
fit2 <- ppm(ants ~ marks + x)
(co <- coef(fit2))
```
```
##   (Intercept)   marksMessor             x 
## -9.5243832518  0.8522118655 -0.0002041438
```
Intensity for the reference type (Cataglyphis):

$\lambda( (x,y) ) = \exp(-9.5243833 + -2.0414381\times 10^{-4} \cdot x)$

Intensity for the other type (Messor):

$\lambda( (x,y) ) = \exp(-9.5243833 + 0.8522119 + -2.0414381\times 10^{-4} \cdot x)$
Fit the model ppm(ants ~ marks * x) and write down an expression for the fitted intensity function.
```
fit3 <- ppm(ants ~ marks * x)
(co <- coef(fit3))
```
```
##   (Intercept)   marksMessor             x marksMessor:x 
## -9.605698e+00  9.676854e-01  1.107981e-05 -3.071343e-04
```
Intensity for the reference type (Cataglyphis):

$\lambda( (x,y) ) = \exp(-9.605698 + 1.1079805\times 10^{-5} \cdot x)$

Intensity for the other type (Messor):

$\lambda( (x,y) ) = \exp(-9.605698 + 0.9676854 + (1.1079805\times 10^{-5} + 0.9676854) \cdot x)$

Compute the fitted intensities of the three models fitted above using predict and plot the results.

pred <- c(predict(fit1), predict(fit2), predict(fit3))
plot(as.solist(pred), ncols = 2, main = "")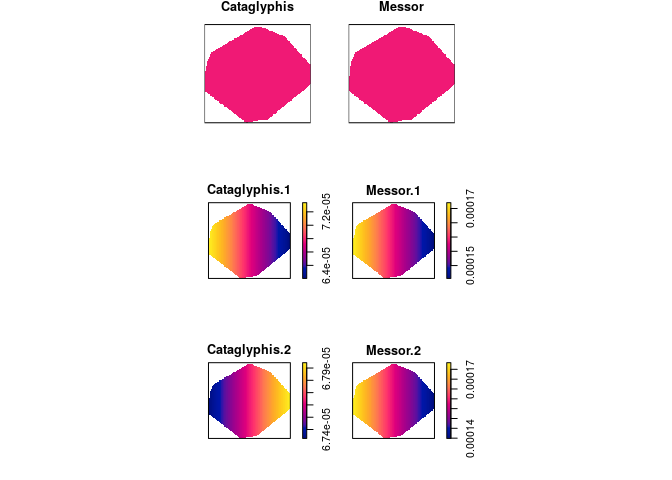

Explain the difference between the models fitted by ppm(ants ~ marks + x) and ppm(ants ~ marks * x) .

For the additive model the effect of the x coordinate is the same for both types of ants, while the effect of x differs in the multiplicative model.

Exercise 12

The study region for the ants’ nests data ants is divided into areas of “scrub” and “field”. We want to fit a Poisson model with different intensities in the field and scrub areas.

The coordinates of two points on the boundary line between field and scrub are given in ants.extra$fieldscrub. First construct a function that determines which side of the line we are on:

fs <- function(x,y) {
  ends <- ants.extra$fieldscrub
  angle <- atan(diff(ends$y)/diff(ends$x))
  normal <- angle + pi/2
  project <- (x - ends$x[1]) * cos(normal) + (y - ends$y[1]) * sin(normal)
  factor(ifelse(project > 0, "scrub", "field"))
}

Now fit the models:

ppm(ants ~ marks + side, data = list(side=fs))
ppm(ants ~ marks * side, data = list(side=fs))

and interpret the results.

fit1 <- ppm(ants ~ marks + side, data = list(side=fs))
fit2 <- ppm(ants ~ marks * side, data = list(side=fs))

In the first model the fitted intensity is lower in the scrub than in the field (but this effect is not significant).

In the second model the fitted intensity of Cataglyphis is lower in the scrub than the intensity of Cataglyphis in the field, where as it is the other way around for Messor. When we allow for the different effect between ant types the scrub/field covariate is significant.